Grundlagen der schnellen Fourier Transformation (FFT)
Die mathematische Transformation
In der Mathematik versteht man unter einer Transformation die Abbildung einer Punktmenge (Wertebereich) in eine andere Punktmenge (Bildbereich). Die Abbildung geschieht mittels einer genau definierten Transformationsvorschrift.
Solche Transformationen können dabei helfen, diverse mathematische Probleme einfacher lösen zu können oder sind manchmal sogar der einzige Lösungsweg.
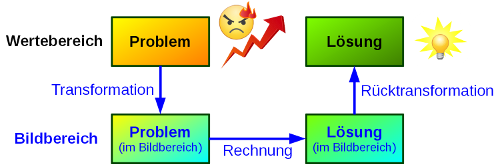
Abbildung: Problemlösung durch mathematische Transformation
Einfache Transformationen, die jeder kennt, sind beispielsweise die Verschiebung, Skalierung, Drehung oder Streckung. Aber auch die logarithmische Skalierung der Achsen eines Koordinatensystems ist eine Transformation. Sie macht es möglich, in Schaubildern Bereiche über mehrere Größenordnungen kompakt darzustellen.
Besondere Bedeutung haben Transformationen, die invertierbar (d.h. umkehrbar) sind. Eine nicht invertierbare Transformation kann manchmal durch die Beschränkung des Wertebereichs invertierbar gemacht werden.
In Zeiten von Computer und Digitalisierung werden diskrete Transformationen besonders häufig eingesetzt. Diskrete Transformationen gehen von endlichen Punktmengen aus und werden genutzt, um Transformationen auf dem Computer berechnen zu können. Dabei spielt die Wahl eines geeigneten Implementationsalgorithmus eine entscheidende Rolle, denn dadurch kann eine Menge an Rechenzeit gespart werden.
Die Fourier Analyse
Die Fourier Analyse ist ein
Teilbereich der Mathematik. Sie befasst sich mit der
Fourier-Transformation, Fourier Reihen und Fourier
Integralen.
Es geht dabei um die Transformation von Funktionen oder
Punktmengen von einem Definitionsbereich in den
Bildbereich. In der Praxis handelt es sich häufig um
zeitabhängige Funktionen.
Deren Definitionsbereich wird daher auch als Zeitbereich bezeichnet. Der
Bildbereich trägt
üblicherweise die Bezeichnung Frequenzbereich. Diese
Bezeichnungen beruhen auf der
Tatsache, dass mit Hilfe der Fourier Transformation ein
zeitabhängiges Signal in sein
Frequenzspektrum zerlegt
werden kann. Darin liegt auch die häufigste technische
Anwendung der
Fourier Analyse.
Die Fourier Analyse besagt, dass jede periodische Funktion f(t) aus einer Reihe von Sinusfunktionen generiert werden kann. Die Frequenzen, Amplituden und Phasen dieser Sinusfunktionen werden als Spektrum der Funktion f(t) bezeichnet.
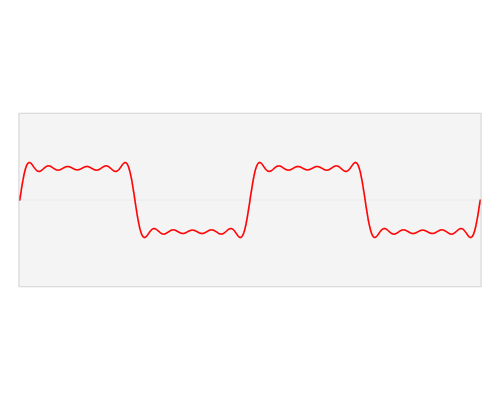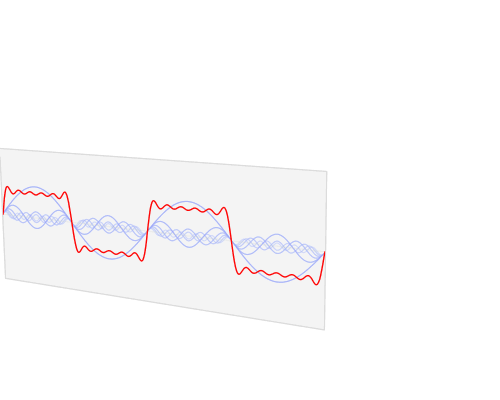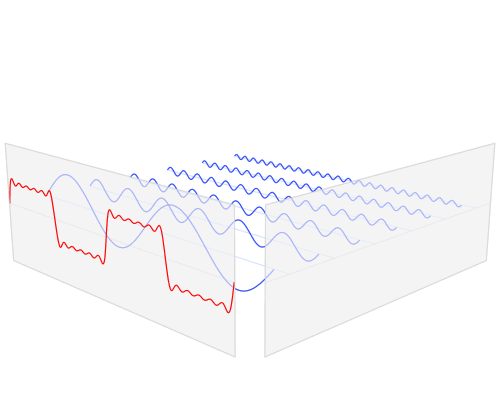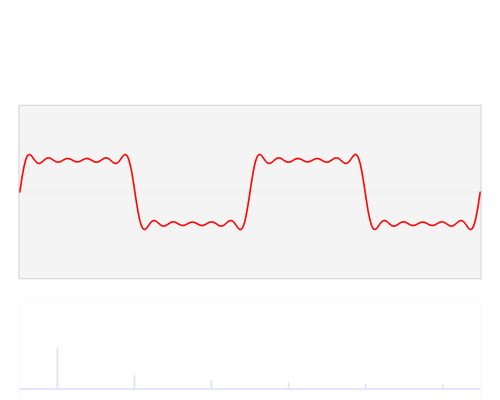
Abbildung: Visualisierung der Fourier Analyse eines Signals
Die diskrete Fourier Transformation
Die diskrete Fourier Transformation (DFT) befasst sich mit der Fourier Analyse von Funktionen, die aus einer endlichen Punktmenge bestehen.
Das Signal auf welches die DFT angewendet werden soll, besteht aus einer Folge äquidistant abgetasteter Werte. Diese werden durch die DFT in den Frequenzbereich transformiert. Die Transformation liefert dann Informationen über das Spektrum des Signals. Durch die inverse DFT kann das Signal wieder aus dem Frequenzbereich in den Zeitbereich rücktransformiert werden.
In der Praxis der digitalen Signalverarbeitung hat man es fast ausschließlich mit solchen Signalen zu tun. Die DFT findet hier Anwendung bei der Spektralanalyse des Signals aber auch beim Entwurf digitaler Filter zur Signalformung.
Die mathematische Definition der DFT
Gegeben sei ein (komplexwertiges) Array A (Vektor) mit n Stützstellen. Die Abtastintervalle des Arrays sind äquidistant.
![]() Gleichung
Gleichung
Die DFT von A ist dann definiert durch:
![]() Gleichung
Gleichung
Die so erhaltenen X(k) sind komplexe Zahlen und heißen Fourierkoeffizienten oder Fourierkomponenten.
Häufig sind die Signale, die mit der DFT analysiert werden sollen reellwertig. Für reelle Signale ergeben sich weitere Symmetrien bei den Fourierkoeffizienten. Ein Teil der Koeffizienten lässt sich durch komplexe Konjugation berechnen. Die Koeffizienten sind "komplex-konjugiert symmetrisch zur Mittenfrequenz".
![]() Gleichung
Gleichung
Beispiel:
![]()
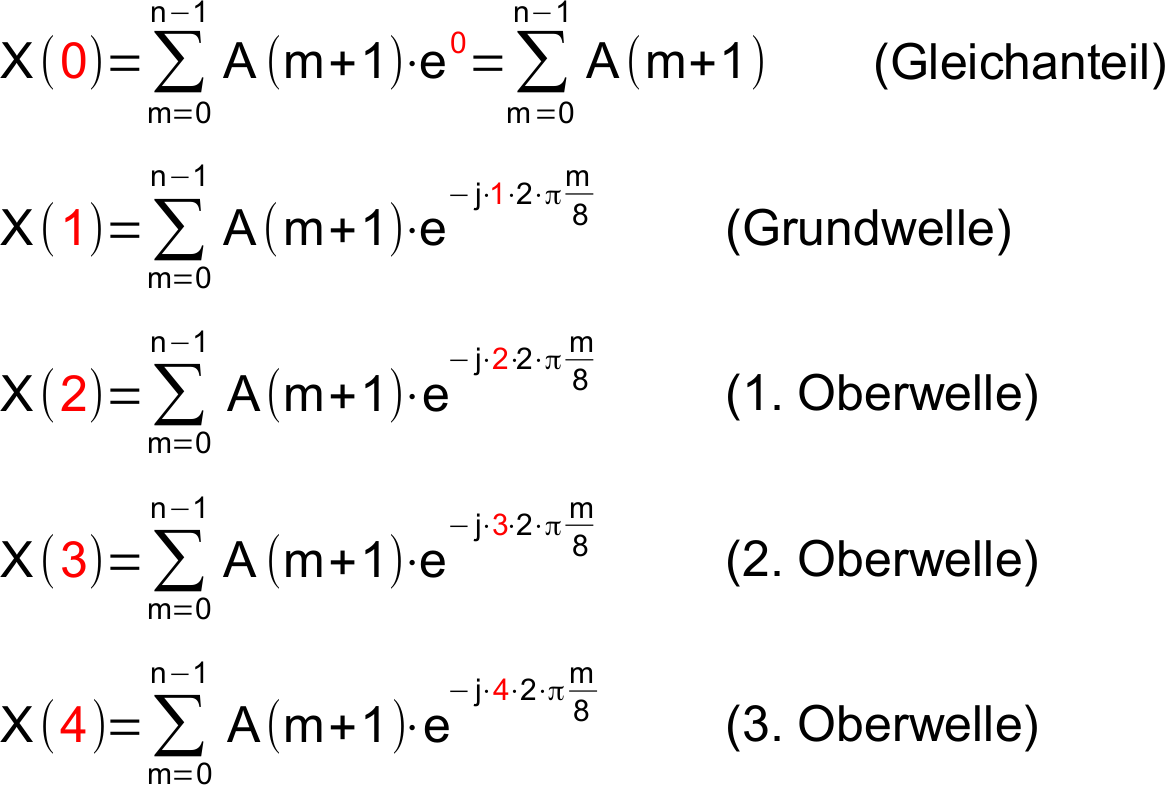
Was passiert bei der DFT eines reellen Signals?
Grundlage für die DFT ist die komplexe Exponentialfunktion. Diese lässt sich in Real- und Imaginärteil zerlegen.
![]() Gleichung
Gleichung
Dabei sind:
f die Frequenz ω die Kreisfrequenz
![]() Gleichung
Gleichung
Wir betrachten nun die Gleichungen im obigen Beispiel für ein Signal, das aus 8 reellwertigen Abtastwerten besteht. Achtung! Die Nummerierung der Abtastwerte beginnt bei Null (und geht bis 7)!
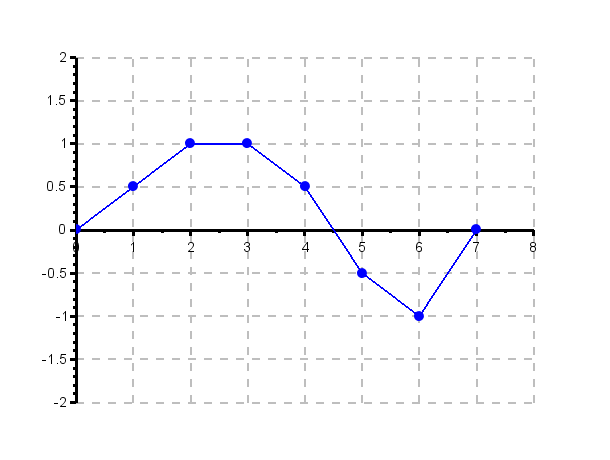
Vergleicht man die komplexe Exponentialfunktion in den Summen für die einzelnen Fourierkoeffizienten mit Gleichung 3.4 so erhält man Analogien zur Frequenz:
![]() Gleichung
Gleichung
Die Frequenz, der im k'ten Fourierkoeffizienten enthaltenen komplexen Exponentialfunktion ist also k, der Funktionswert wird an der Stelle t=m/n genommen. Die komplexe Exponentialfunktion lässt sich in Real- und Imaginärteil zerlegen, welche Kreisfunktionen mit der Frequenz k sind.
Anschaulich gesehen, passiert bei der DFT also folgendes:
0. Fourierkoeffizient
Der 0'te Fourierkoeffizient, auch als Gleichanteil bezeichnet, entspricht der Summe der Abtastwerte des Signals.
![]() Gleichung
Gleichung
Der k'te Fourierkoeffizient, entspricht der Summe der Abtastwerte multipliziert mit einer Kreisfunktion der Frequenz k.
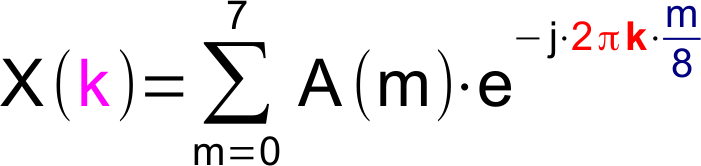 Gleichung
Gleichung
Dies kann man sich grafisch aus den folgenden Bildern klar machen:
1. Fourierkoeffizient
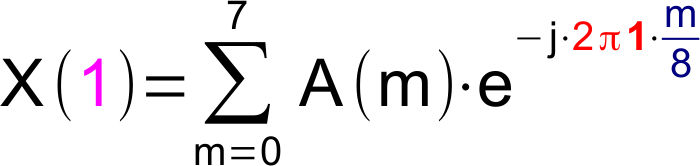 Gleichung
Gleichung
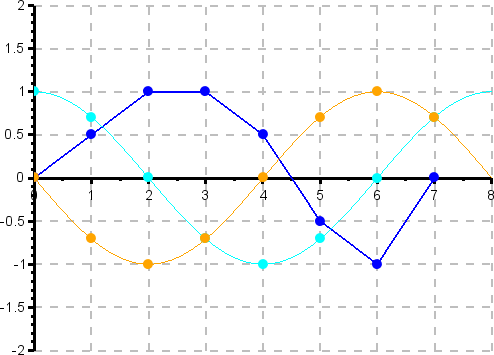
Grafische Darstellung der Berechnung des ersten (k=1) Fourierkoeffizienten (Grundwelle). Das Signal (blau) wird an den Stützstellen mit der Gewichtungsfunktion für den Realteil (türkis) bzw. für den Imaginärteil (orange) multipliziert und die Produkte werden aufsummiert. Die Wellenlänge (Periode) der Gewichtungsfunktion entspricht dem gesamten Abtastintervall.
2. Fourierkoeffizient
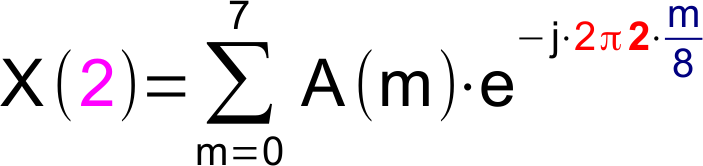 Gleichung
Gleichung
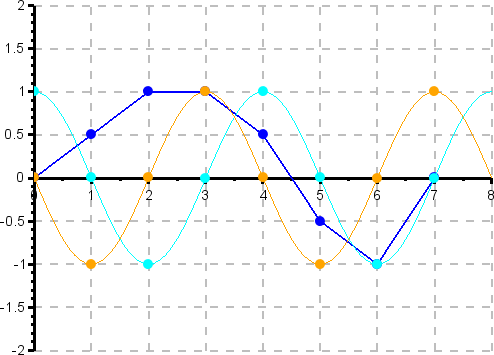
Grafische Darstellung der Berechnung des zweiten (k=2) Fourierkoeffizienten (1. Oberwelle oder 1. Harmonische). Das Signal (blau) wird an den Stützstellen mit der Gewichtungsfunktion für den Realteil (türkis) bzw. für den Imaginärteil (orange) multipliziert und die Produkte werden aufsummiert. Die Frequenz der Gewichtungsfunktion ist das Doppelte der Grundfrequenz.
3. Fourierkoeffizient
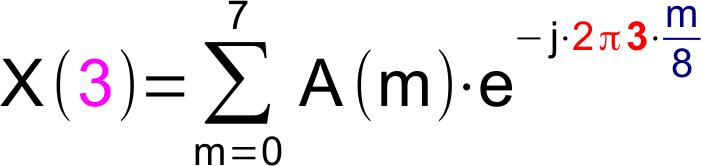 Gleichung
Gleichung
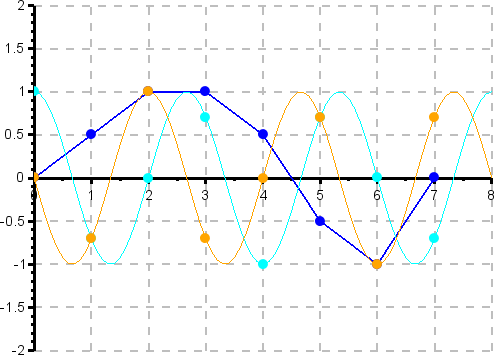
Grafische Darstellung der Berechnung des dritten (k=3) Fourierkoeffizienten (2. Oberwelle oder 2. Harmonische). Das Signal (blau) wird an den Stützstellen mit der Gewichtungsfunktion für den Realteil (türkis) bzw. für den Imaginärteil (orange) multipliziert und die Produkte werden aufsummiert. Die Frequenz der Gewichtungsfunktion ist das 3-Fache der Grundfrequenz.
4. Fourierkoeffizient
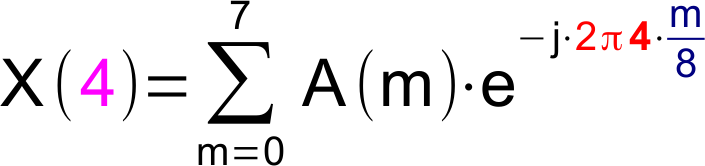 Gleichung
Gleichung
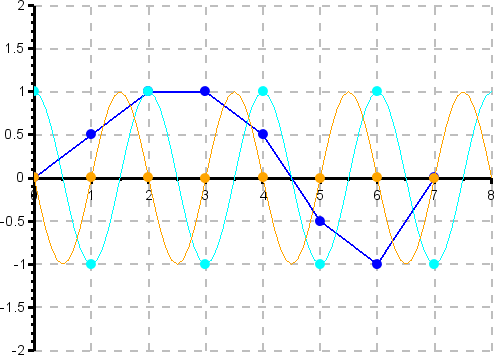
Grafische Darstellung der Berechnung des vierten (k=4) Fourierkoeffizienten (3. Oberwelle oder 3. Harmonische). Das Signal (blau) wird an den Stützstellen mit der Gewichtungsfunktion für den Realteil (türkis) bzw. für den Imaginärteil (orange) multipliziert und die Produkte werden aufsummiert. Die Frequenz der Gewichtungsfunktion ist das 4-Fache der Grundfrequenz.
5. bis 7. Fourierkoeffizient
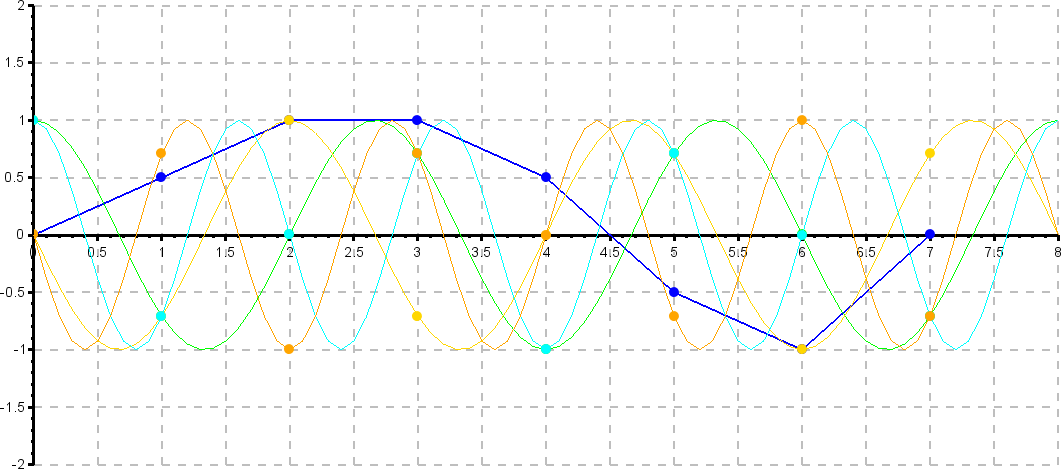
Grafische Darstellung der Berechnung des 5 (k=5) Fourierkoeffizienten (4. Oberwelle oder 4. Harmonische). Die Frequenz der Gewichtungsfunktion ist das 5-Fache der Grundfrequenz. Die Stützstellen des Realteils (türkis) fallen mit den Stützstellen der 2. Oberwelle (grün) zusammen. Die Stützstellen des Imaginärteils (orange) liegen spiegelverkehrt zu den Stützstellen der 2. Oberwelle (gelb). Der 5. Fourierkoeffizient ist also komplex konjugiert zum 3. Fourierkoeffizienten.
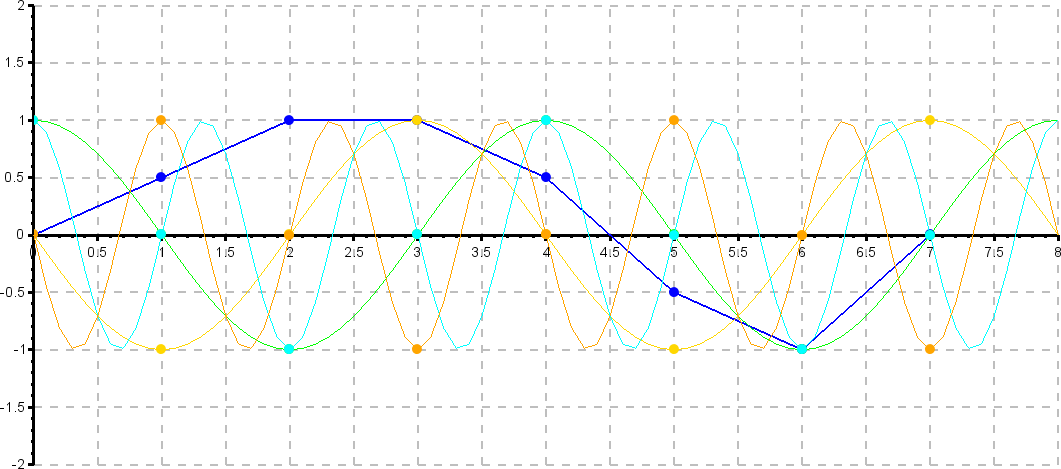
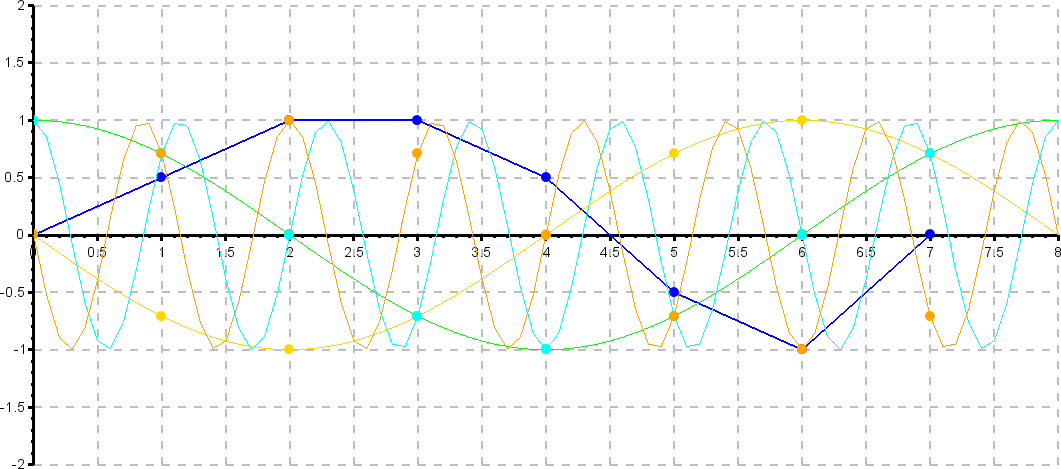
Grafische Darstellung der Berechnung des 6. und 7. (k=6 und k=7) Fourierkoeffizienten.
Der Frequenzgang als Ergebnis der DFT
Die Fourierkoeffizienten sind ein komplexer Vektor, der als Frequenzgang oder auch Spektrum bezeichnet wird. Bei reellen Signalen weist der Frequenzgang eine Symmetrie um die Mitte auf. Der Vektor der Absolutwerte der Fourierkoeffizienten wird auch als Amplitudengang bezeichnet. Der Vektor der Phasenwinkel wird als Phasengang bezeichnet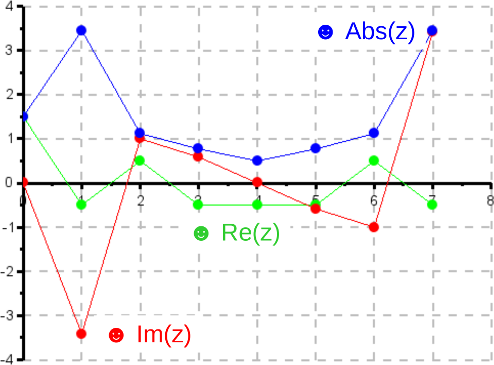
Grafische Darstellung der Fourierkoeffizienten (Frequenzgang) und deren Beträgen (Amplitudengang).
Interpretation der DFT
Das Ergebnis der DFT zeigt nun, welche Frequenzen wie
stark im Signal vertreten sind.
Dies ist hilfreich, wenn beispielsweise Auswirkungen
eines Übertragungskanals, dessen
Frequenzgang beschränkt ist, auf das Signal vorhergesagt
werden sollen.
Aber nicht nur auf Signale lässt sich die DFT anwenden.
Es können auch komplexe physikalische
Systeme untersucht werden, deren Verhalten dann
mit der DFT analysiert werden kann.
Allgemein kann man sagen, dass Signale, deren Werte sich zeitlich schnell und stark ändern, immer auch mit hohen Frequenzen verbunden sind. Insbesondere bei Signalen muss der Übertragungskanal diese hohen Frequenzen auch zulassen. Andernfalls wird das Signal beim Empfänger stark verfälscht. Im worst Case ist das Signal beim Empfänger nicht mehr rekonstruierbar.
Die inverse DFT
Kennt man den mit der DFT berechneten Frequenzgang eines Signals, kann man mit der inversen DFT (IDFT) den Zeitverlauf des Signals rekonstruieren.
![]() Gleichung
Gleichung
Vergleicht man die obige Definitionsgleichung der IDFT mit der Definitionsgleichung für die DFT (Gleichung 3.2), fällt auf, dass diese sich durch ein Minuszeichen im Exponenten unterscheiden. Dazu kommt der Gewichtungsfaktor 1/n.
Dies folgt aus einer grundlegenden Eigenschaft der Exponentialfunktion, die für beliebige Zahlen z gilt:
![]() Gleichung
Gleichung
Das rekonstruierte Zeitsignal A(n) setzt sich dann aus mehreren Kreisfunktionen, deren Frequenzen Vielfache der Grundfrequenz sind, zusammen. Die Amplituden der erzeugenden Kreisfunktionen ergeben sich aus den Fourierkoeffizienten.
Was passiert bei der IDFT eines reellen Signals?
Als Beispiel betrachten wir das reellwertige Ausgangssignal von dem wir mit Hilfe der DFT das Spektrum berechnet haben:
![]() Gleichung
Gleichung
Das berechnete Spektrum lautet:
![]() Gleichung
Gleichung
Um zu erkennen, welche Auswirkungen die einzelnen Spektralanteile auf das rücktransformierte Signal haben, setzen wir Teile des Spektrums gleich Null und betrachten die IDFT.
Der Gleichanteil
Betrachten wir die IDFT des Gleichanteils:
![]() Gleichung
Gleichung
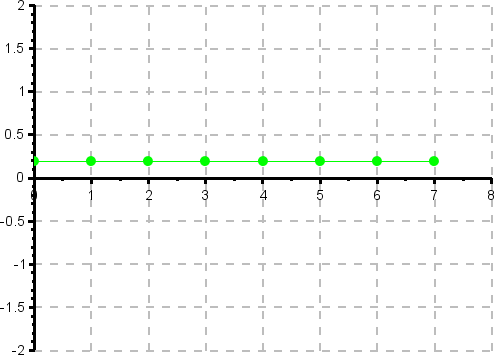
IDFT des Gleichanteils
Es handelt sich um ein reellwertiges, konstantes Signal. Das Signal entspricht dem Mittelwert des Eingangssignals A(k).
Die Grundwelle
Betrachten wir die IDFT der Grundwelle:
![]() Gleichung
Gleichung
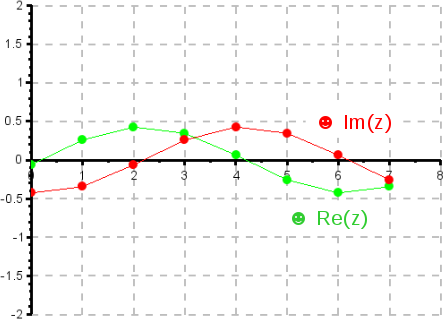
IDFT der Grundwelle
Man sieht, dass es sich dabei um ein komplexes Signal handelt, das aus zwei phasenverschobenen Kreisfunktionen der Grundfrequenz besteht.
Die zur Grundwelle symmetrische Oberwelle
Da das Spektrum eines reellwertigen Signals eine Symmetrie um die Mittenfrequenz aufweist, betrachten wir nun die IDFT der zur Grundwelle symmetrischen Oberwelle:
![]() Gleichung
Gleichung
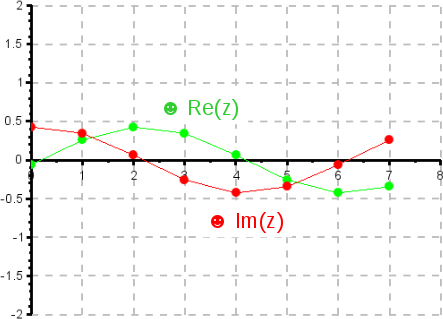
IDFT der zur Grundwelle symmetrischen Oberwelle
Auch hier handelt es sich um ein komplexes Signal, das aus zwei phasenverschobenen Kreisfunktionen der Grundfrequenz besteht. Vergleicht man mit der IDFT der Grundwelle, stellt man fest, dass die Realteile übereinstimmen, die Imaginärteile um eine halbe Wellenlänge phasenverschoben sind.
Grundwelle + symmetrische Oberwelle
Überlagert man die IDFTs der Grundwelle und der symmetrischen Oberwelle, erhält man ein reellwertiges Signal, da sich die phasenverschobenen Imaginärteile aufheben.
![]() Gleichung
Gleichung
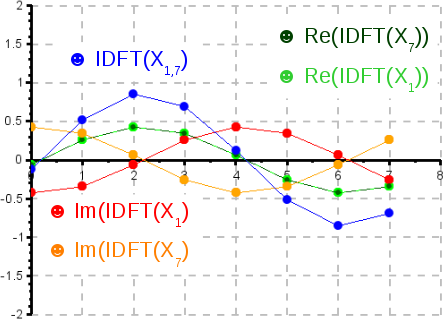
IDFT der zur Grundwelle symmetrischen Oberwelle
Überlagerung der restlichen Oberwellen
Nach dem gleichen Prinzip erhalten wir die Überlagerung der restlichen Oberwellen und ihrer symmetrischen Anteile.
![]() Gleichung
Gleichung
![]() Gleichung
Gleichung
![]() Gleichung
Gleichung
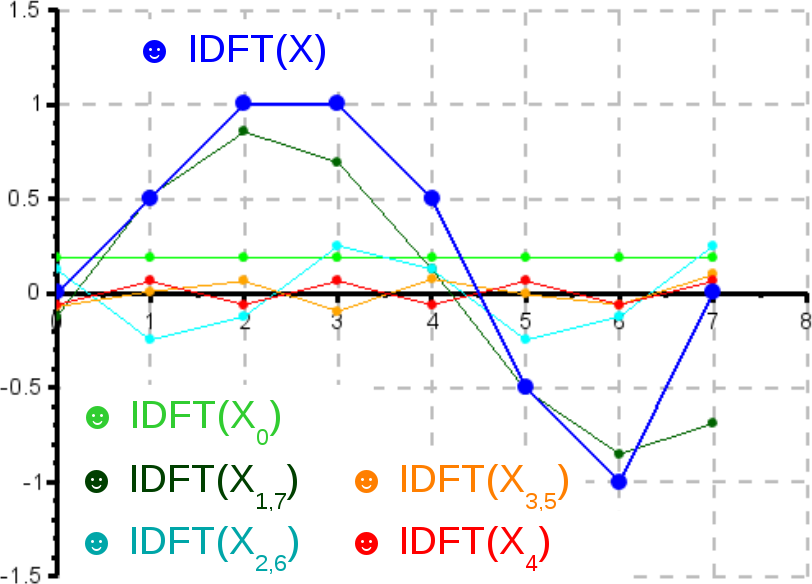
Superposition aller Anteile des Spektrums
Die nachfolgende Abbildung zeigt die spektrale Zusammensetzung eines Signals, das sich nur langsam ändert.
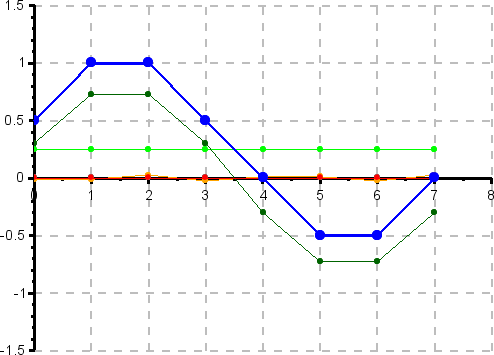
Spektrale Zusammensetzung eines langsam veränderlichen Signals
Die Spektralanalyse zeigt, dass das Signal praktisch nur aus einem Gleichanteil und der Grundwelle besteht. Oberwellen sind fast nicht vorhanden.
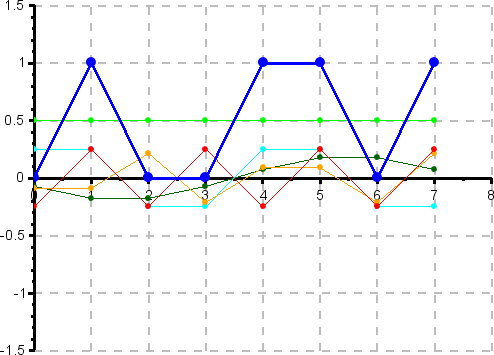
Spektrale Zusammensetzung eines schnell veränderlichen Signals
Im Gegensatz zum langsam veränderlichen Signal zeigt ein schnell veränderliches Signal einen hohen Oberwellenanteil.
Die FFT
Die Abkürzung FFT steht für fast Fourier transform. Die schnelle Fourier Transformation ist ein optimierter Algorithmus, der es erlaubt eine diskrete Fourier Transformation (DFT) in einem Bruchteil der Zeit zu berechnen. Die moderne Digitale Signalverarbeitung wäre ohne die FFT nicht denkbar, da Echtzeit-Verfahren ohne die Effizienz der FFT aufgrund der langen Rechenzeiten nicht machbar wären.Rechenaufwand DFT vs. FFT
Der Rechenaufwand einer DFT mit N Stützstellen ist:
![]() Gleichung
Gleichung
Der Rechenaufwand einer FFT mit N Stützstellen ist:
![]() Gleichung
Gleichung
Als Zeitgewinn kann man das Verhältnis der Rechenzeit von DFT zu FFT sehen.
![]()
![]() Gleichung
Gleichung
Bei einem Datensatz mit n=210=1024 Stützstellen errechnet man beispielsweise bereits einen Zeitgewinn von ungefähr Faktor 100. Bei größeren Datensätzen sind die Zeitgewinne deutlich höher.